Understanding gradience
\[ \newcommand{\expr}[3]{\begin{array}{c} #1 \\ \bbox[lightblue,5px]{#2} \end{array} ⊢ #3} \newcommand{\ct}[1]{\bbox[font-size: 0.8em]{\mathsf{#1}}} \newcommand{\updct}[1]{\ct{upd\_#1}} \newcommand{\abbr}[1]{\bbox[transform: scale(0.95)]{\mathtt{#1}}} \newcommand{\pure}[1]{\bbox[border: 1px solid orange]{\bbox[border: 4px solid transparent]{#1}}} \newcommand{\return}[1]{\bbox[border: 1px solid black]{\bbox[border: 4px solid transparent]{#1}}} \def\P{\mathtt{P}} \def\Q{\mathtt{Q}} \def\True{\ct{T}} \def\False{\ct{F}} \def\ite{\ct{if\_then\_else}} \def\Do{\abbr{do}} \]
One of the most striking findings from experimental semantics and pragmatics is the pervasiveness of gradience in aggregated measures.1 While semanticists have long recognized the existence of gradience in some domains–e.g. gradable adjectives–we often assume categorical distinctions in other domains–e.g. factivity. And even where traditional approaches assume categorical distinctions, experimental methods often reveal continuous variation. For the reasons laid out above, understanding this gradience is crucial for developing theories that connect formal semantics to behavioral data.
Examples of Potentially Unexpected Gradience
The kinds of distributionally and inferentially defined properties we develop generalizations around are not always readily apparent in large-scale datasets. An example we will look at in-depth in our second case study of the course is that, when attempting to measure veridicality/factivity, we end up with more gradience than we might have expected. We can illustrate this using the MegaAttitude datasets.
Figure 1 shows veridicality judgments collected by White and Rawlins (2018) as part of their MegaVeridicality dataset.

One thing White and Rawlins (2018) note is the apparent gradience in these measures. This gradience presents a challenge if we want to use these measures to evaluate generalizations about the relationship between two properties. For instance, say we are interested in understanding the relationship betwen factivity and neg(ation)-raising. A predicate is neg-raising if it gives rise to inferences of the form from (1) to (2):
- Jo doesn’t think that Mo left.
- Jo thinks that Mo didn’t leave.
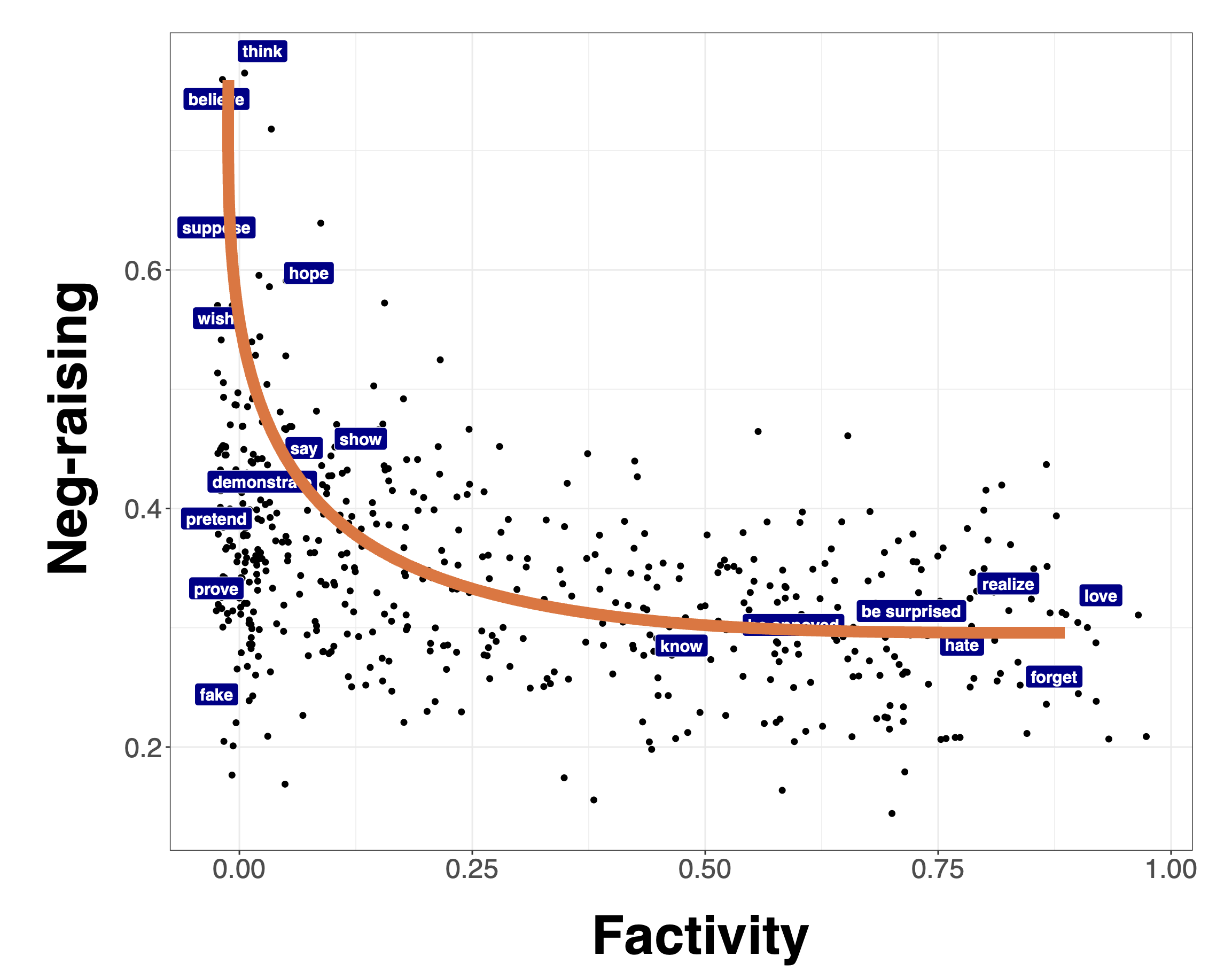
One way of deriving a factivity measure from the MegaVeridicality dataset is to take the max along both dimensions, as shown in Figure 2. The idea here is that, it will give rise to veridicality inferences with both positive and negative matrix polarity.

Now let’s suppose we’re interested in generalizations about the relationship between two measures. For instance, maybe want to evaluate the relationship between factivity and neg-raising, where we might tend to suspect that factives are not neg-raisers.
Figure 3 shows a comparison of the measure of neg(ation)-raising from the MegaNegRaising dataset collected by An and White (2020) and the derived factivity measure from the MegaVeridicality dataset collected by White and Rawlins (2018).
The challenge is that, once we move to relating continuous measures, rather than categorical distinctions, we don’t know what the relationship between measures should look like in any particular case. To illustrate, let’s consider another example. Anand and Hacquard (2014) propose that, if a predicate gives rise to inferences about both beliefs and preferences, it backgrounds the belief inferences. To evaluate this hypothesis, we might try to derive a measure of belief inferences and preference inferences and then relate them.
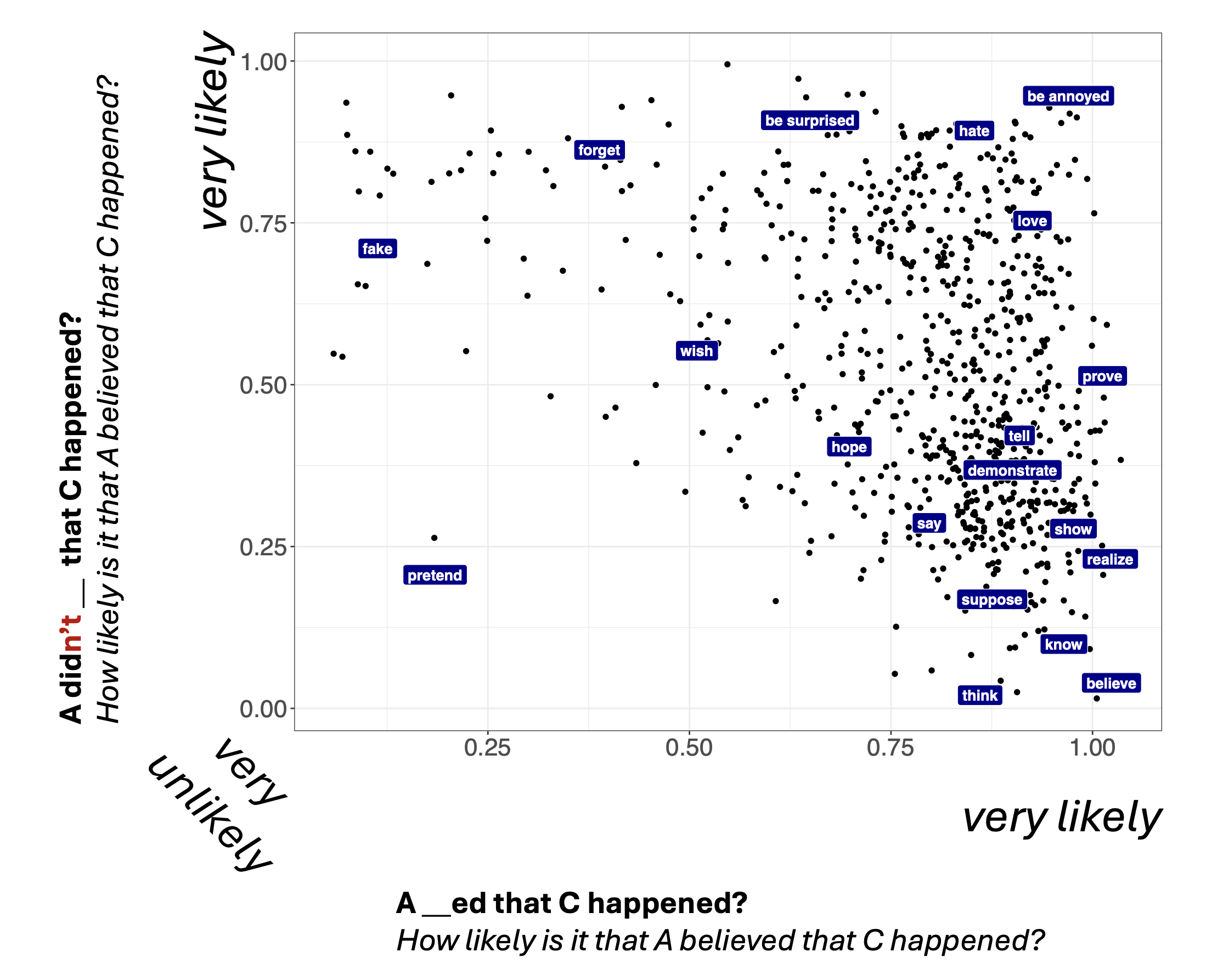
To this end, we can use the MegaIntensionality dataset collected by Kane, Gantt, and White (2022). Figure 4 shows a measure of belief inferences and Figure 5 shows a measure of desire inferences.
And Figure 6 shows a comparison of the desire and belief measures.
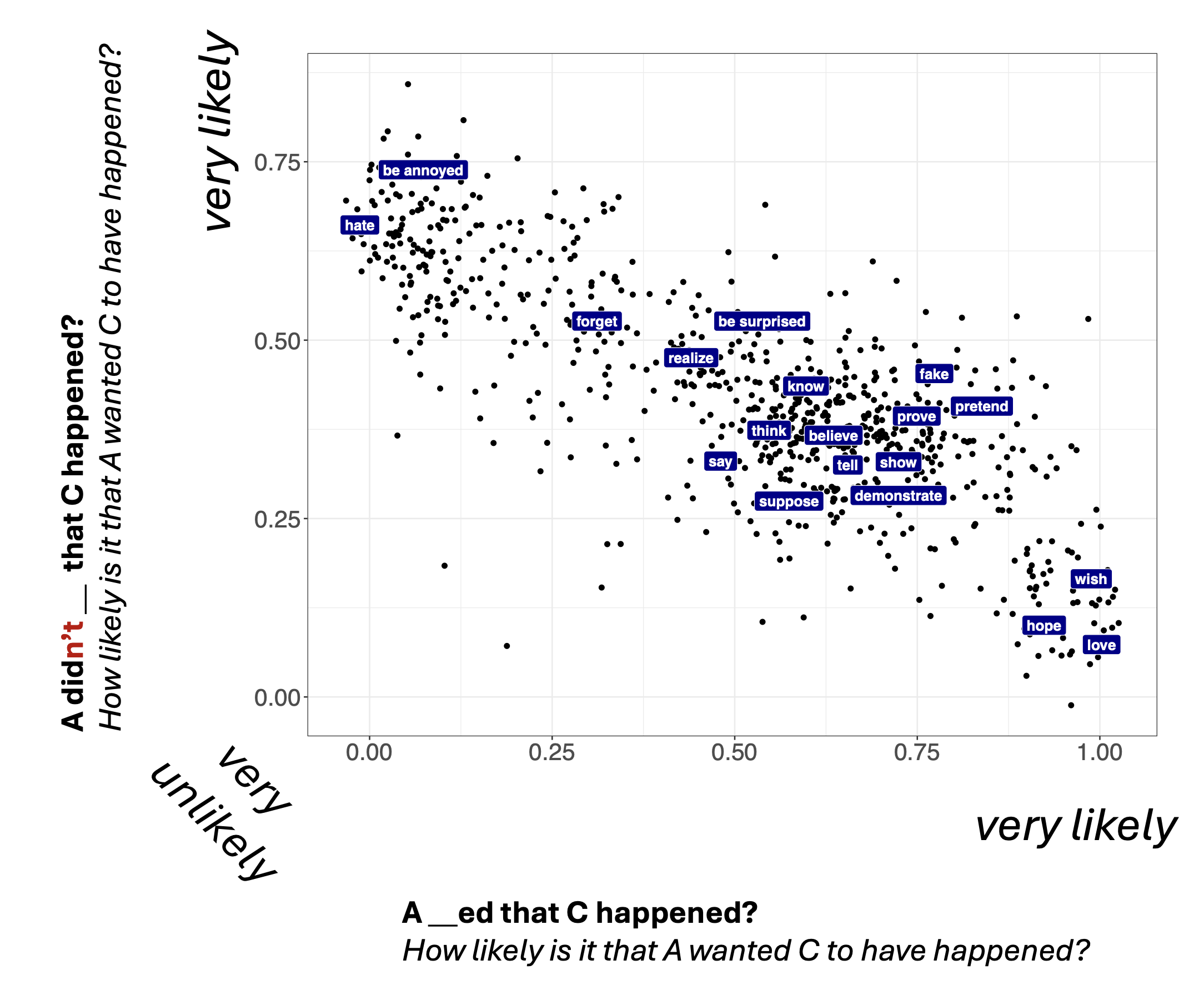
Figure 6 show the relationship between these two measures.
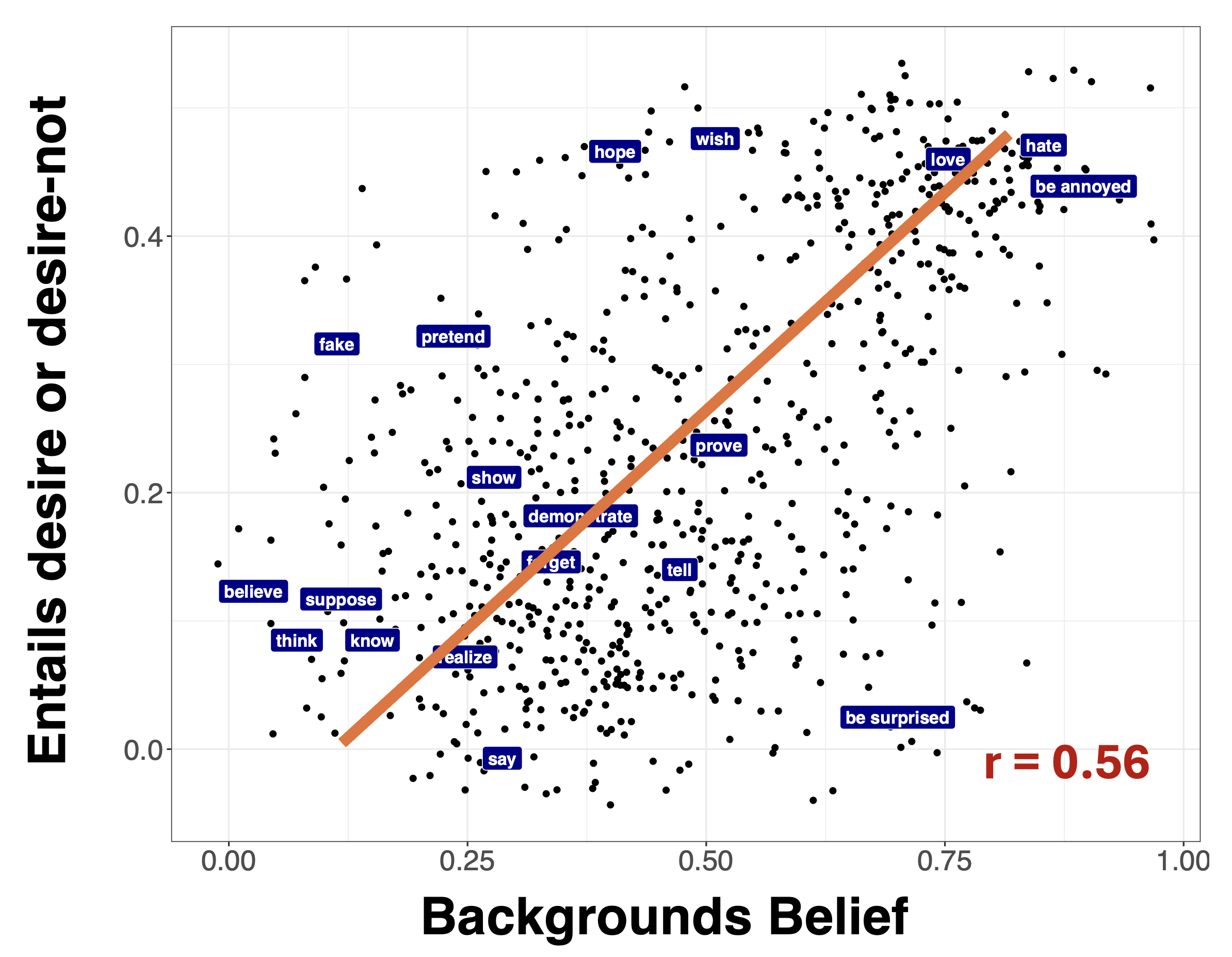
There are two main takeaways from this example. First, the generalization proposed by@anand_factivity_2014 is indeed supported by the data. Second, the relationship between these two measures is strikingly different from the relationship we observe between the continuous measures of factivity and neg-raising. We need some way of theorizing about these continuous relationships.
Two Fundamental Types of Uncertainty
The framework we’ll explore distinguishes two general types of uncertainty that can produce gradience: resolved (or type-level) uncertainty and unresolved (or token-level) uncertainty, both of which can arise from multiple sources.
Sources of Gradience in Inference Judgments
├── Resolved (Type-Level) Uncertainty
│ ├── Ambiguity
│ │ ├── Lexical (e.g., "run" = locomote vs. manage)
│ │ ├── Syntactic (e.g., attachment ambiguities)
│ │ └── Semantic (e.g., scope ambiguities)
│ └── Discourse Status
│ └── QUD (Question Under Discussion)
└── Unresolved (Token-Level) Uncertainty
├── Vagueness (e.g., height of a "tall" person)
├── World knowledge (e.g., likelihood that facts are true)
└── Task effects
├── Response strategies
└── Response errorResolved Uncertainty: Multiple Discrete Possibilities
Resolved uncertainty arises when speakers must choose among discrete interpretations. Consider (3):
- My uncle is running the race.
The verb run is ambiguous—the uncle might be a participant (locomotion) or the organizer (management). Asked “How likely is it that my uncle has good managerial skills?”, participants who interpret run as locomotion might respond near 0.2, while those interpreting it as management might respond near 0.8. The population average might be 0.5, but this reflects a mixture of discrete interpretations, not genuine gradience.
This uncertainty is “resolved” because once speakers fix an interpretation, the inference follows determinately. The gradience emerges from averaging across different resolutions, not from uncertainty within any single interpretation.
A similar phenomenon is observable with anaphora. Consider (4):
- Whenever anyone laughed, the magician scowled and their assistant smirked. They were secretly pleased.
One is quite likely to infer from (4) that the magician’s assistant is secretly pleased, but not necessarily that the magician is pleased, even though, in principle, it may be that both are, or even that only the magician is. Ultimately, the ambiguity is resolved when we fix the referent.
Unresolved Uncertainty: Gradient Within Interpretations
Unresolved uncertainty contrasts with resolved uncertainty in that it persists even after fixing all ambiguities. Consider (5):
- My uncle is tall.
Even with no ambiguity about tall’s meaning, speakers remain uncertain whether the uncle exceeds any particular height threshold. This is classic vagueness—the predicate’s application conditions are inherently gradient (Fine 1975; Graff 2000; Kennedy 2007; Rooij 2011; Sorensen 2023).
World knowledge creates another layer: even knowing someone runs races (locomotion sense), we remain uncertain about their speed, endurance, or likelihood of finishing. These uncertainties appear within individual trials, not just across participants.
Why This Distinction Matters
The type of uncertainty has profound implications for semantic theory:
- Resolved uncertainty suggests discrete semantic representations with probabilistic selection
- Unresolved uncertainty suggests gradient representations or probabilistic reasoning within fixed meanings
Different phenomena may involve different uncertainty types. As we’ll see, vagueness seems to give rise to unresolved uncertainty (the conditions of application of tall seem inherently uncertain), while factivity’s gradience is perhaps more puzzling: is it resolved uncertainty from ambiguous predicates, or unresolved uncertainty in projection itself?
References
Footnotes
In this course, we will focus mainly on gradience in aggregated inference judgments, but there is a deep literature on gradience in acceptability judgments within the experimental syntax literature (Bard, Robertson, and Sorace 1996; Keller 2000; Sorace and Keller 2005; Sprouse 2007, 2011; Featherston 2005, 2007; Gibson and Fedorenko 2010, 2013; Sprouse and Almeida 2013; Sprouse, Schütze, and Almeida 2013; Schütze and Sprouse 2014; Lau, Clark, and Lappin 2017; Sprouse et al. 2018).↩︎