From theory to data
\[ \newcommand{\expr}[3]{\begin{array}{c} #1 \\ \bbox[lightblue,5px]{#2} \end{array} ⊢ #3} \newcommand{\ct}[1]{\bbox[font-size: 0.8em]{\mathsf{#1}}} \newcommand{\updct}[1]{\ct{upd\_#1}} \newcommand{\abbr}[1]{\bbox[transform: scale(0.95)]{\mathtt{#1}}} \newcommand{\pure}[1]{\bbox[border: 1px solid orange]{\bbox[border: 4px solid transparent]{#1}}} \newcommand{\return}[1]{\bbox[border: 1px solid black]{\bbox[border: 4px solid transparent]{#1}}} \def\P{\mathtt{P}} \def\Q{\mathtt{Q}} \def\True{\ct{T}} \def\False{\ct{F}} \def\ite{\ct{if\_then\_else}} \def\Do{\abbr{do}} \]
Semantic theory has achieved remarkable success in characterizing the compositional structure of natural language meaning. Through decades of careful theoretical work, semanticists have developed elegant formal systems that capture how complex meanings arise from the systematic combination of simpler parts. These theories explain two fundamental types of judgments that speakers make: acceptability judgments about whether strings are well-formed, and inference judgments about what follows from what speakers say.
The field now stands at an exciting juncture. The rise of large-scale experimental methods and computational modeling opens new opportunities to test and refine these theoretical insights against rich behavioral data. The challenge—and opportunity—is to connect our elegant formal theories to the messy, gradient patterns we observe when hundreds of speakers make thousands of judgments. How can we maintain the theoretical insights that formal semantics has achieved while extending them to account for this new empirical richness?
Probabilistic Dynamic Semantics (PDS) aims to provide a systematic bridge between these theoretical insights and behavioral data. It takes the compositional analyses developed using traditional Montagovian methods and maps them to probabilistic models that can be quantitatively evaluated against experimental results. The goal is not to replace traditional semantics but to extend its reach, allowing us to test theoretical predictions at unprecedented scale while maintaining formal rigor.
Traditional Semantic Methodology: Foundations of Success
Semanticists study the systematic relationships between linguistic expressions and the inferences they support. The field’s methodology centers on two types of judgments:
Acceptability judgments assess whether strings are well-formed relative to a language and in a particular context of use (Chomsky 1957; see Schütze 2016). For example, in a context where a host asks what a guest wants with coffee, (1) is clearly acceptable, while (2) is not Sprouse and Villata (2021):
- What would you like with your coffee?
- #What would you like and your coffee?
Inference judgments assess relationships between strings (see Davis and Gillon 2004). When speakers hear (3), they typically infer (4) (White 2019):
- Jo loved that Mo left.
- Mo left.
Observational Adequacy
A core desideratum for semantic theories is observational adequacy (Chomsky 1964): for any string \(s \in \Sigma^*\), we should predict how acceptable speakers find it in context, and for acceptable strings \(s, s'\), we should predict whether speakers judge \(s'\) inferable from \(s\). Achieving observational adequacy requires mapping vocabulary elements to abstractions that predict judgments parsimoniously.
These abstractions may be discrete or continuous, simple or richly structured. Through careful analysis of consistent inference patterns, semanticists have identified powerful generalizations. For instance, examining predicates like love, hate, be surprised, and know, theorists observed they all give rise to inferences about their complement clauses that survive under negation and questioning. This led to positing that they all share a property that predicts systematic inferential behavior across diverse predicates (Kiparsky and Kiparsky 1970; cf. Karttunen 1971).
Descriptive Adequacy and Theoretical Depth
Beyond observational adequacy lies descriptive adequacy: capturing data “in terms of significant generalizations that express underlying regularities in the language” (Chomsky 1964, 63). This drive for deeper explanation motivates the field’s emphasis on parsimony and formal precision.
The history of generative syntax illustrates two approaches to achieving descriptive adequacy:
- Analysis-driven: Start with observationally adequate analyses in expressive formalisms, then extract generalizations as constraints
- Hypothesis-driven: Begin with constrained formalisms (like CCG or minimalist grammars) and test their empirical coverage
The hypothesis-driven approach, which PDS adopts for semantics, aims to delineate phenomena through representational constraints. This becomes crucial when developing models that both accord with theoretical assumptions and can be evaluated quantitatively (Baroni 2022; Pavlick 2023).
The Power and Natural Boundaries of Traditional Methods
This methodology has yielded profound insights into semantic composition, scope phenomena, discourse dynamics, and the semantics-pragmatics interface more generally. By focusing on carefully constructed examples and native speaker intuitions, theorists have uncovered deep regularities in how meaning is constructed and interpreted.
Yet every methodology has natural boundaries. Traditional semantic methods excel at identifying patterns and building theories but face practical constraints when we ask:
- How well do our generalizations, based on examining 5-10 predicates, extend to the thousands of predicates in the lexicon?
- What factors beyond semantic knowledge influence the judgments we observe?
- How exactly does abstract semantic knowledge produce concrete behavioral responses?
The Experimental Turn: New Opportunities for Semantic Theory
The traditional methodology’s success has created a foundation solid enough to support exciting new extensions. Experimental semantics brings the tools of behavioral experimentation to bear on questions about meaning, allowing us to test and refine theoretical insights at unprecedented scale.
Scaling Semantic Investigation
Where traditional methods might examine a handful of predicates, experimental approaches can investigate entire lexical domains. Extending our example involving the verb love: English has thousands of similar clause-embedding predicates, each potentially varying in its inferential properties. We can now test whether generalizations based on canonical examples extend across these vast lexicons.
The MegaAttitude project (White and Rawlins 2016, 2018, 2020; White et al. 2018; An and White 2020; Moon and White 2020; Kane, Gantt, and White 2022) is one example of this approach. This project aims to collect inference judgments for hundreds of predicates across multiple contexts and inference types. This scale reveals patterns that are very difficult to see and evaluate the quality of using traditional methods—subtle distinctions between near-synonyms, unexpected predicate clusters, and systematic variation across semantic domains.
Teasing Apart Contributing Factors
Experimental methods also allow us to investigate the rich array of factors that influence inference judgments:
- Semantic knowledge: The core meanings of expressions
- World knowledge: Prior beliefs about plausibility
- Contextual factors: The discourse context and QUD
- Individual differences: Variation in how speakers interpret expressions
- Response strategies: How participants use rating scales
Rather than viewing these as confounds, we can see them as windows into the cognitive processes underlying semantic interpretation. For instance, Degen and Tonhauser (2021) systematically manipulated world knowledge to show how prior beliefs modulate the strength of factive inferences, revealing the interplay between semantic and pragmatic factors.
Making Linking Hypotheses Explicit
Perhaps most importantly, experimental approaches force us to make explicit what traditional methods leave implicit: the link between semantic representations and behavioral responses (Jasbi, Waldon, and Degen 2019; Waldon and Degen 2020; Phillips et al. 2021). When we say speakers judge that an inference follows, what cognitive processes produce that judgment? How do abstract semantic representations map onto the responses on some scale?
This is not merely a methodological detail—it’s a substantive theoretical question. Different linking hypotheses make different predictions about response patterns, allowing us to test not just our semantic theories but our assumptions about how those theories connect to behavior. Even if our real interest is in characterizing the semantic representations of speakers, we can’t ignore the way those representations map onto their responses in some task.
Understanding Gradience: A Taxonomy of Uncertainty
One of the most striking findings from experimental semantics is the pervasiveness of gradience in aggregated measures. While semanticists have long recognized the existence of gradience in some domains–e.g. gradable adjectives–we often assume categorical distinctions in other domains–e.g. factivity. And even where traditional approaches assume categorical distinctions, experimental methods often reveal continuous variation. For the reasons laid out above,understanding this gradience is crucial for developing theories that connect formal semantics to behavioral data.
Examples of Potentially Unexpected Gradience
The kinds of distributionally and inferentially defined properties we develop generalizations around are not always readily apparent in large-scale datasets. An example we will look at in-depth in our second case study of the course is that, when attempting to measure veridicality/factivity, we end up with more gradience than we might have expected. We can illustrate this using the MegaAttitude datasets.
Figure 1 shows veridicality judgments collected by White and Rawlins (2018) as part of their MegaVeridicality dataset.
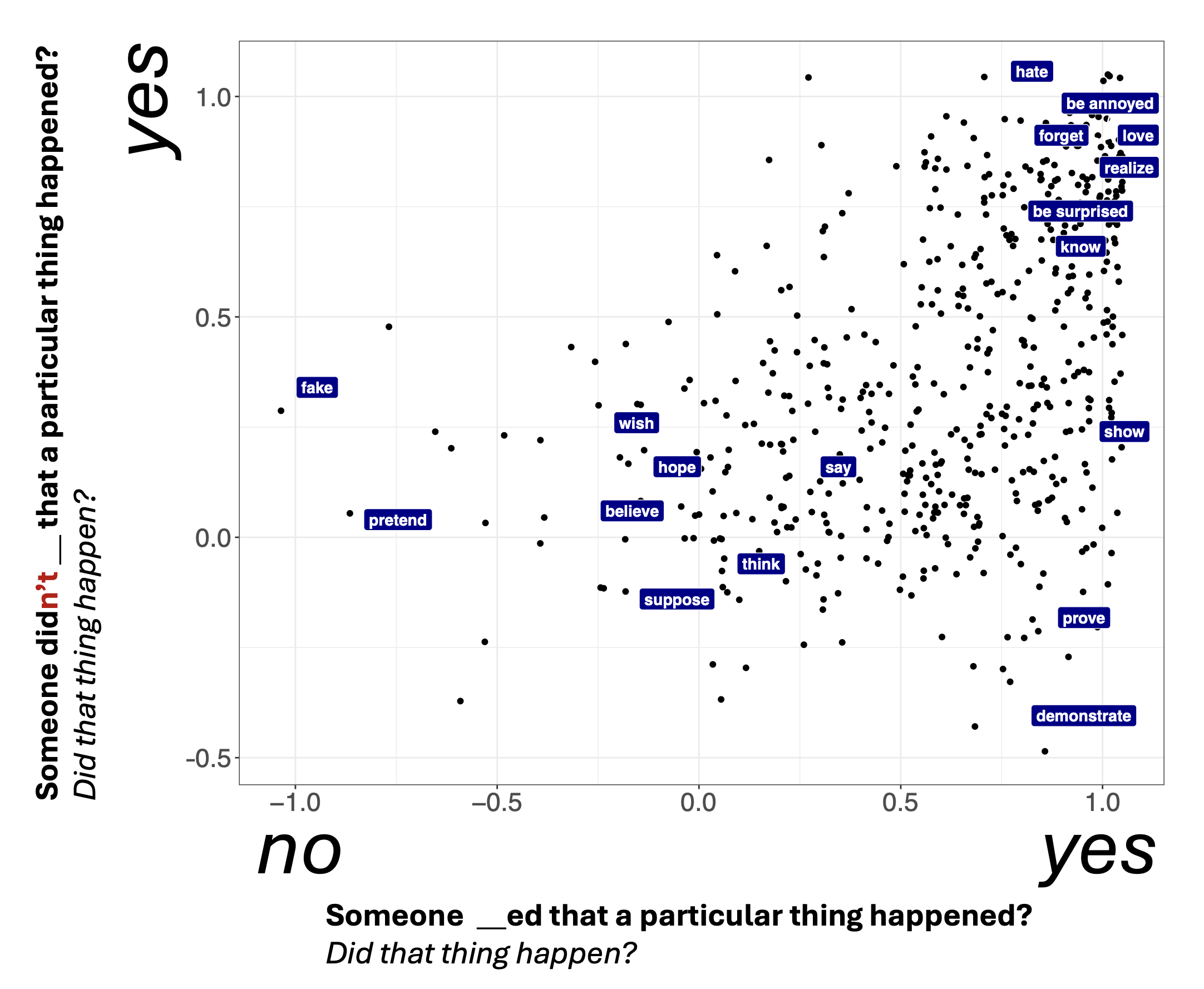
One thing White and Rawlins (2018) note is the apparent gradience in these measures. This gradience presents a challenge if we want to use these measures to evaluate generalizations about the relationship between two properties. For instance, say we are interested in understanding the relationship betwen factivity and neg(ation)-raising. A predicate is neg-raising if it gives rise to inferences of the form from (5) to (6):
- Jo doesn’t think that Mo left.
- Jo thinks that Mo didn’t leave.
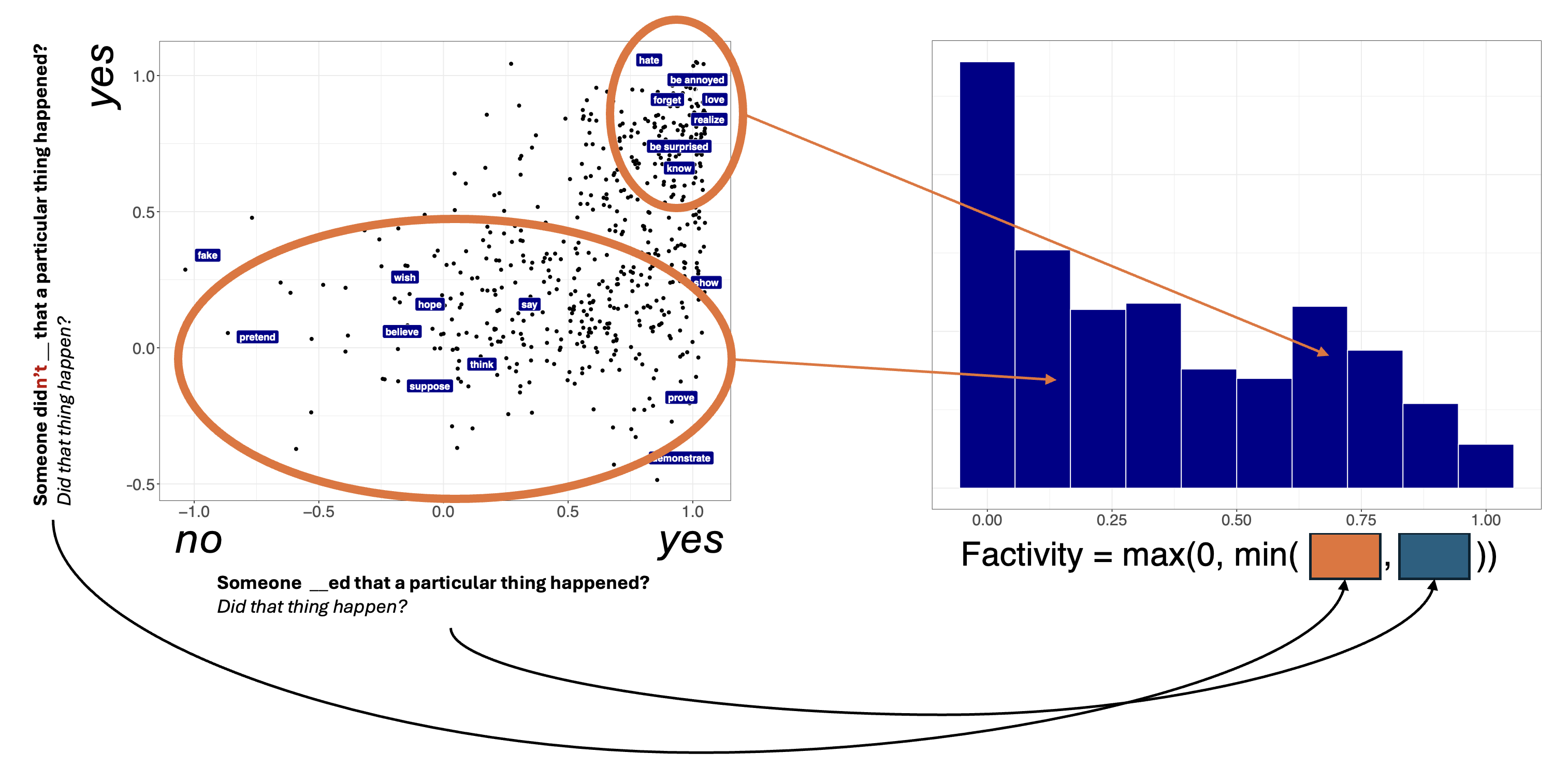
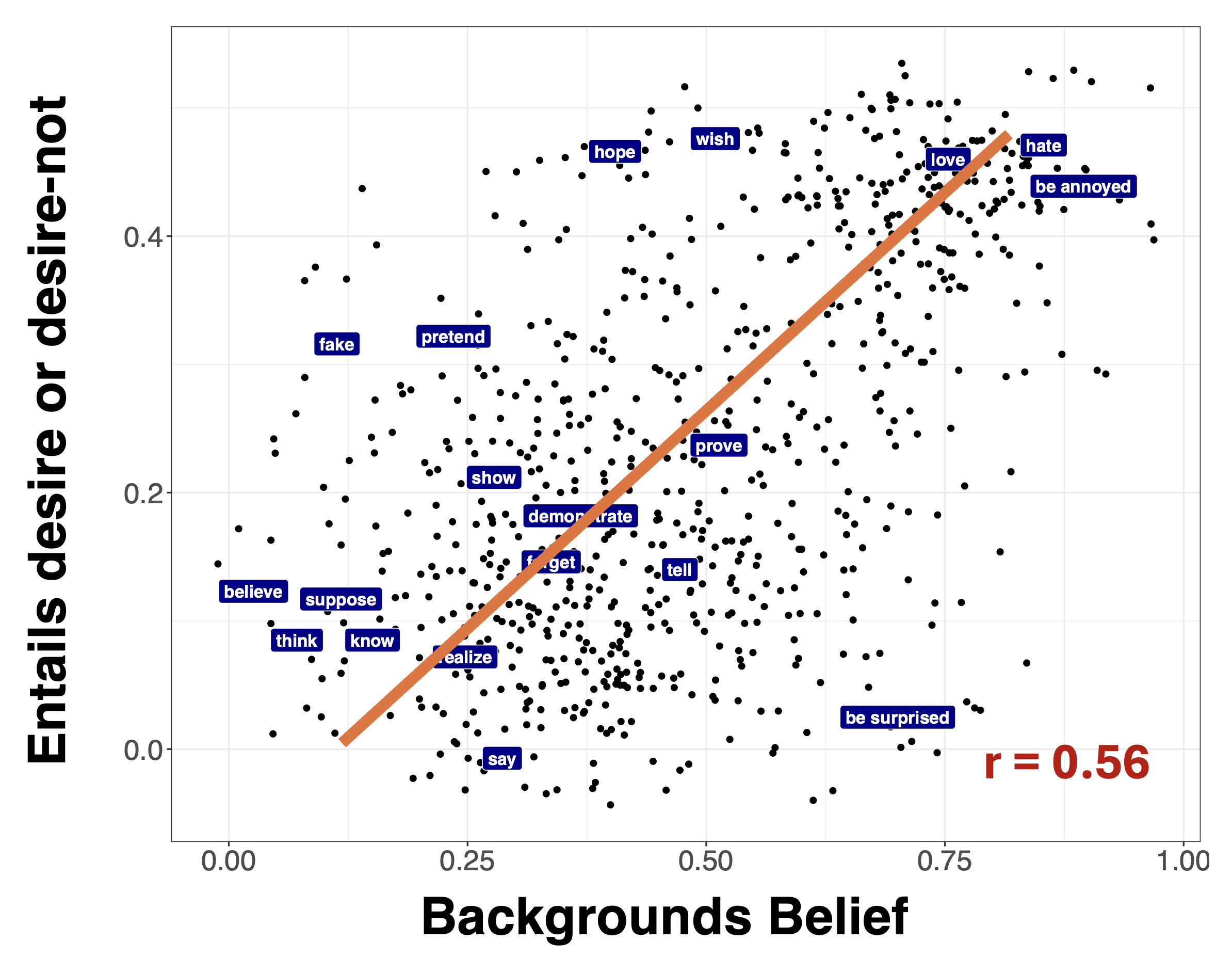
One way of deriving a factivity measure from the MegaVeridicality dataset is to take the max along both dimensions, as shown in Figure 2. The idea here is that, it will give rise to veridicality inferences with both positive and negative matrix polarity.
Now let’s suppose we’re interested in generalizations about the relationship between two measures. For instance, maybe want to evaluate the relationship between factivity and neg-raising, where we might tend to suspect that factives are not neg-raisers.
Figure 3 shows a comparison of the measure of neg(ation)-raising from the MegaNegRaising dataset collected by An and White (2020) and the derived factivity measure from the MegaVeridicality dataset collected by White and Rawlins (2018).
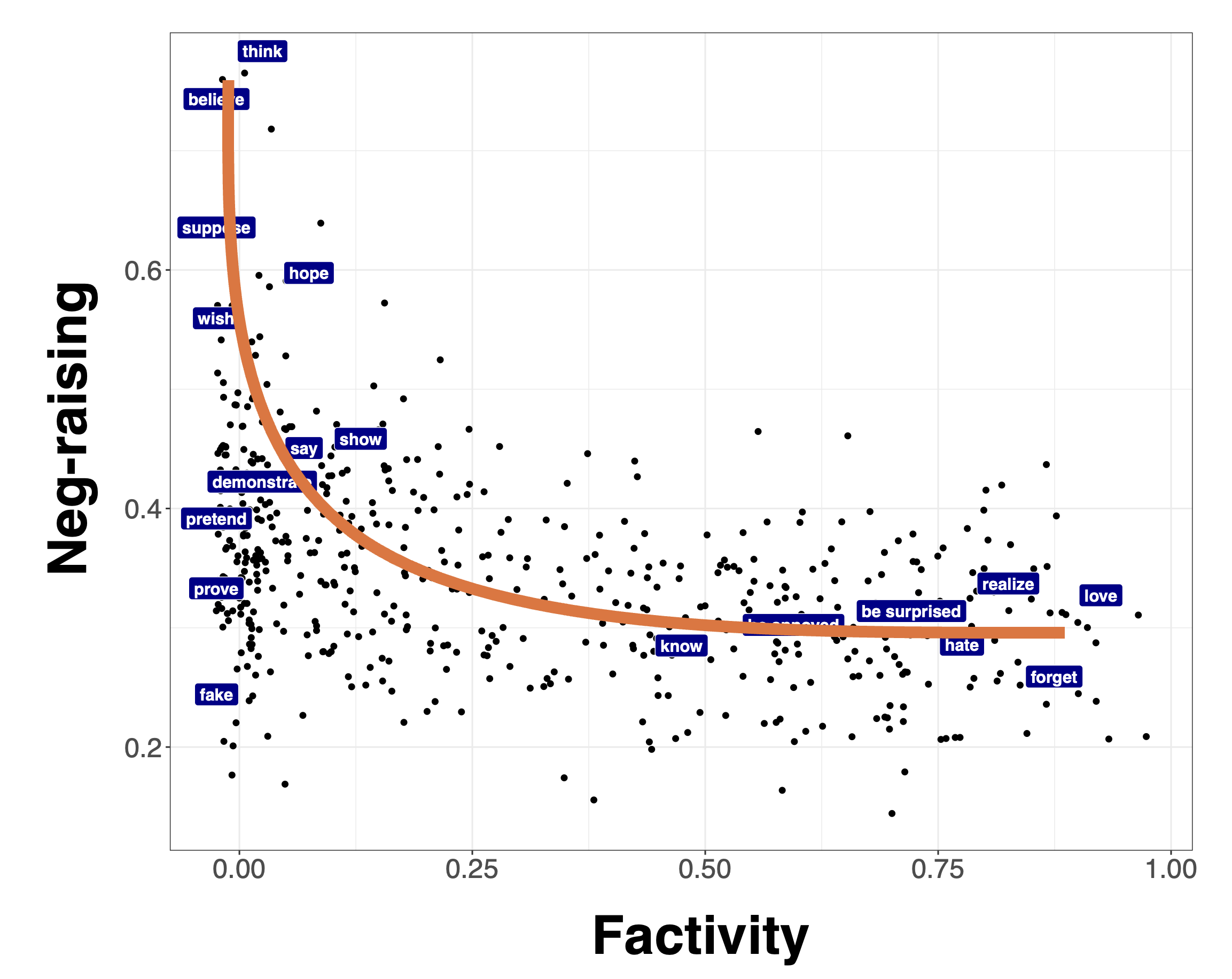
The challenge is that, once we move to relating continuous measures, rather than categorical distinctions, we don’t know what the relationship between measures should look like in any particular case. To illustrate, let’s consider another example. Anand and Hacquard (2014) propose that, if a predicate gives rise to inferences about both beliefs and preferences, it backgrounds the belief inferences. To evaluate this hypothesis, we might try to derive a measure of belief inferences and preference inferences and then relate them.
To this end, we can use the MegaIntensionality dataset collected by Kane, Gantt, and White (2022). Figure 4 shows a measure of belief inferences and Figure 5 shows a measure of desire inferences.
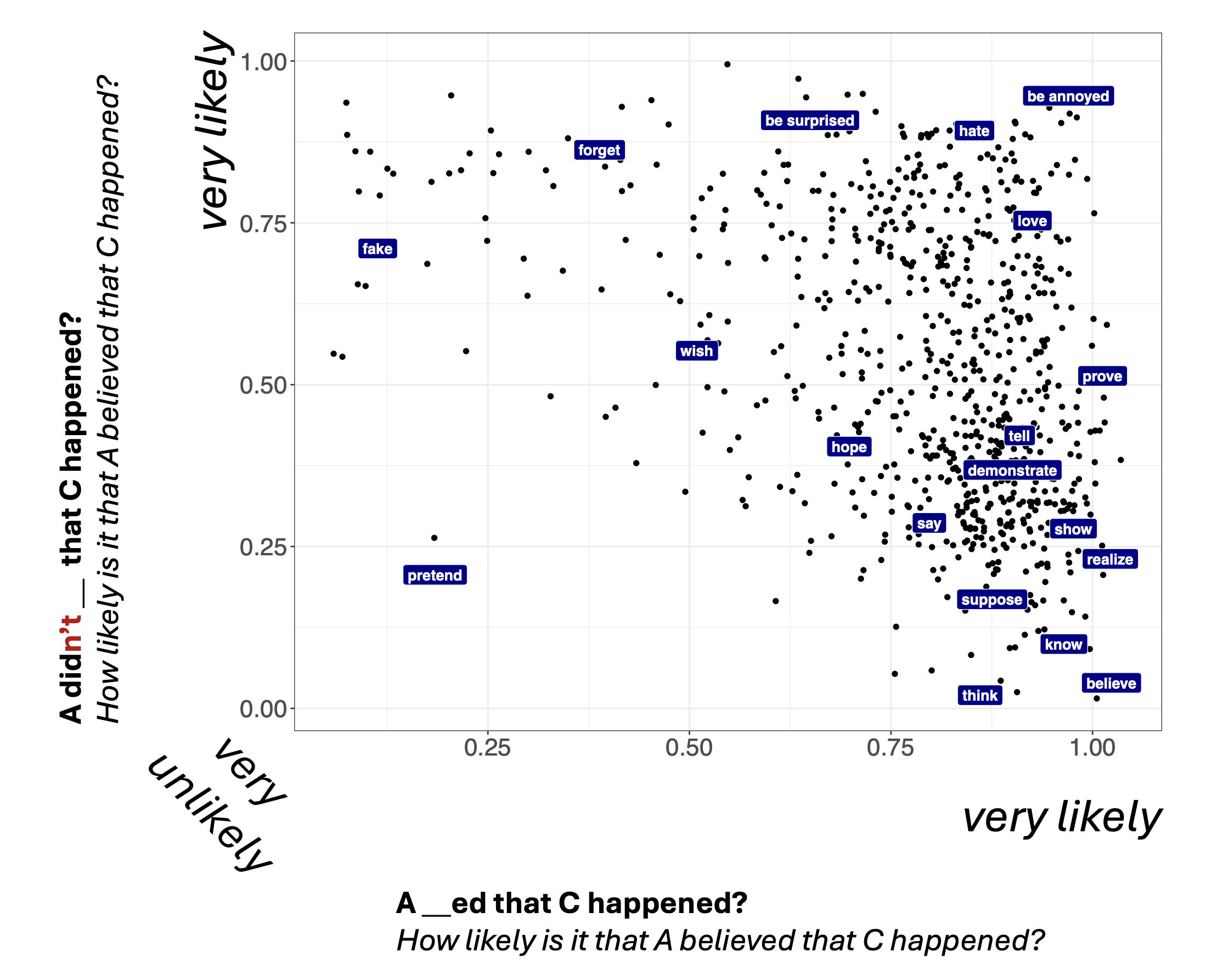
And Figure 6 shows a comparison of the desire and belief measures.
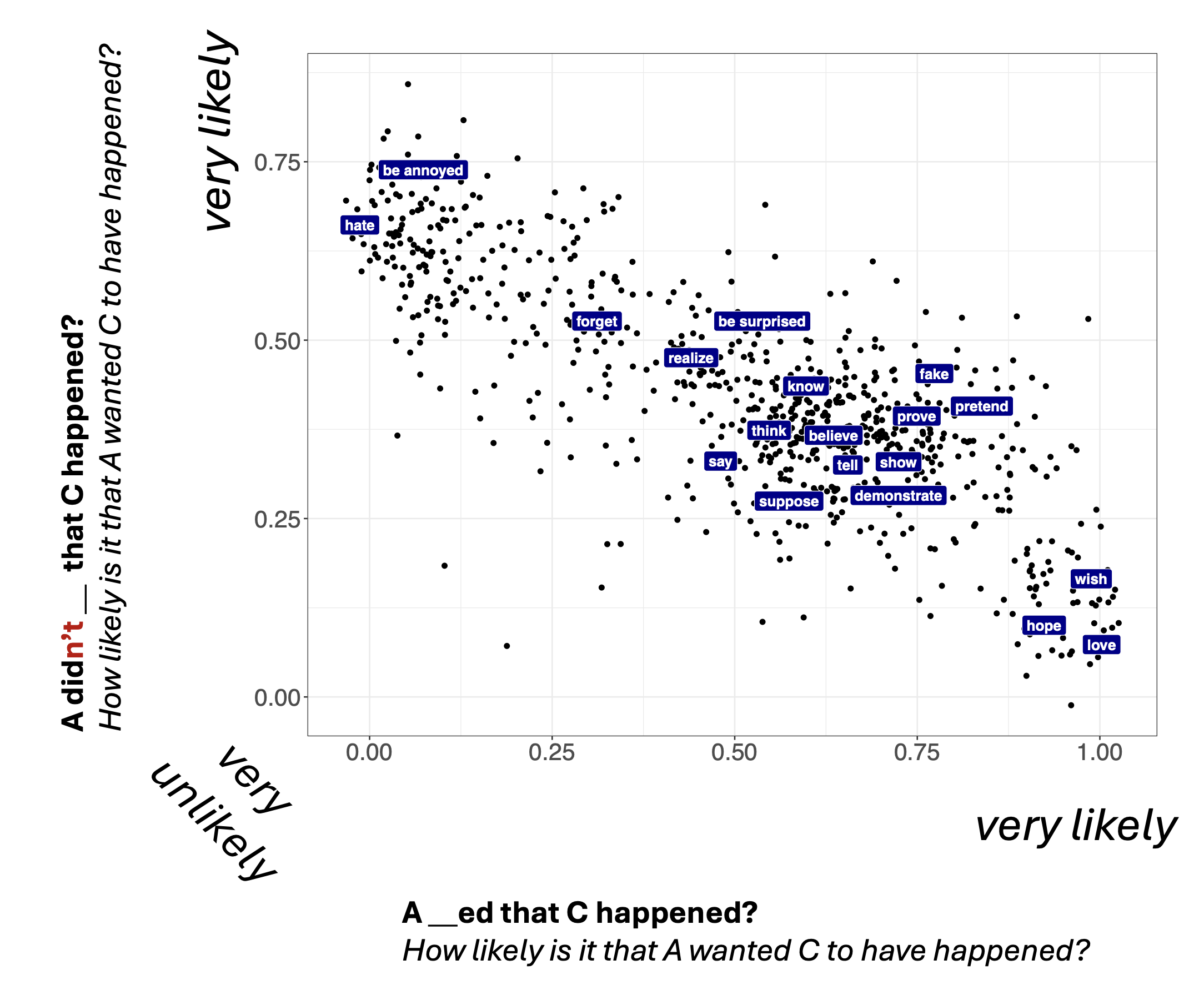
Figure 6 show the relationship between these two measures.
There are two main takeaways from this example. First, the generalization proposed by@anand_factivity_2014 is indeed supported by the data. Second, the relationship between these two measures is strikingly different from the relationship we observe between the continuous measures of factivity and neg-raising. We need some way of theorizing about these continuous relationships.
Two Fundamental Types of Uncertainty
The framework we’ll explore distinguishes two general types of uncertainty that can produce gradience: resolved (or type-level) uncertainty and unresolved (or token-level) uncertainty, both of which can arise from multiple sources.
Sources of Gradience in Inference Judgments
├── Resolved (Type-Level) Uncertainty
│ ├── Ambiguity
│ │ ├── Lexical (e.g., "run" = locomote vs. manage)
│ │ ├── Syntactic (e.g., attachment ambiguities)
│ │ └── Semantic (e.g., scope ambiguities)
│ └── Discourse Status
│ └── QUD (Question Under Discussion)
└── Unresolved (Token-Level) Uncertainty
├── Vagueness (e.g., height of a "tall" person)
├── World knowledge (e.g., likelihood that facts are true)
└── Task effects
├── Response strategies
└── Response errorResolved Uncertainty: Multiple Discrete Possibilities
Resolved uncertainty arises when speakers must choose among discrete interpretations. Consider (7):
- My uncle is running the race.
The verb run is ambiguous—the uncle might be a participant (locomotion) or the organizer (management). Asked “How likely is it that my uncle has good managerial skills?”, participants who interpret run as locomotion might respond near 0.2, while those interpreting it as management might respond near 0.8. The population average might be 0.5, but this reflects a mixture of discrete interpretations, not genuine gradience.
This uncertainty is “resolved” because once speakers fix an interpretation, the inference follows determinately. The gradience emerges from averaging across different resolutions, not from uncertainty within any single interpretation.
A similar phenomenon is observable with anaphora. Consider (8):
- Whenever anyone laughed, the magician scowled and their assistant smirked. They were secretly pleased.
One is quite likely to infer from (8) that the magician’s assistant is secretly pleased, but not necessarily that the magician is pleased, even though, in principle, it may be that both are, or even that only the magician is. Ultimately, the ambiguity is resolved when we fix the referent.
Unresolved Uncertainty: Gradient Within Interpretations
Unresolved uncertainty contrasts with resolved uncertainty in that it persists even after fixing all ambiguities. Consider (9):
- My uncle is tall.
Even with no ambiguity about tall’s meaning, speakers remain uncertain whether the uncle exceeds any particular height threshold. This is classic vagueness—the predicate’s application conditions are inherently gradient (Fine 1975; Graff 2000; Christopher Kennedy 2007; Rooij 2011; Sorensen 2023).
World knowledge creates another layer: even knowing someone runs races (locomotion sense), we remain uncertain about their speed, endurance, or likelihood of finishing. These uncertainties appear within individual trials, not just across participants.
Why This Distinction Matters
The type of uncertainty has profound implications for semantic theory:
- Resolved uncertainty suggests discrete semantic representations with probabilistic selection
- Unresolved uncertainty suggests gradient representations or probabilistic reasoning within fixed meanings
Different phenomena may involve different uncertainty types. As we’ll see, vagueness seems to give rise to unresolved uncertainty (the conditions of application of tall seem inherently uncertain), while factivity’s gradience is perhaps more puzzling: is it resolved uncertainty from ambiguous predicates, or unresolved uncertainty in projection itself?
Case Studies: Testing Semantic Theory at Scale
To illustrate how PDS bridges formal semantics and experimental data, we’ll examine two case studies that exemplify different aspects of the framework.
Case Study 1: Vagueness and Gradable Adjectives
Vague predicates provide an ideal starting point because everyone agrees they involve gradient uncertainty. Expressions like tall, expensive, and old lack sharp boundaries—there’s no precise height at which someone becomes tall (Lakoff 1973; Sadock 1977; Lasersohn 1999; Krifka 2007; Solt 2015).
Formal semantic theories have long recognized this gradience. Degree-based approaches (Klein 1980; Bierwisch 1989; Kamp 1975; Chris Kennedy 1999; Christopher Kennedy and McNally 2005; Christopher Kennedy 2007; Barker 2002) analyze gradable adjectives as expressing relations to contextual thresholds:
- tall is true of \(x\) if \(\ct{height}(x) \geq d_\text{tall}\) (context)
The threshold \(d_\text{tall}\) varies with context—what counts as tall for a basketball player differs from tall for a child. But even within a fixed context, speakers show gradient judgments about borderline cases.
This makes vagueness ideal for demonstrating how PDS works. The framework can: - Maintain the compositional degree-based analysis from formal semantics - Add probability distributions over thresholds to capture gradient judgments - Model how context shifts these distributions - Link threshold distributions to slider scale responses
Recent experimental work reveals additional complexity. Different adjective types show distinct patterns: - Relative adjectives (tall, wide): Maximum gradience in positive form - Absolute adjectives (clean, dry): Different threshold distributions - Minimum vs. maximum standard: Asymmetric patterns of imprecision
These patterns both support and refine formal theories, showing how experimental data can advance theoretical understanding. Recent years have seen partial integration into computational models (Lassiter and Goodman 2013, 2017; Qing and Franke 2014; Kao et al. 2014; Bumford and Rett 2021). We’ll show that PDS allows us to synthesize and compare these different partial approaches.
Case Study 2: Factivity and Projection
While vagueness involves expected gradience, factivity presents a puzzle. Traditional theory treats factivity as discrete—predicates either trigger presuppositions or they don’t (Kiparsky and Kiparsky 1970; Karttunen 1971).1 Yet experimental data reveals pervasive gradience.
A predicate is factive if it triggers inferences about its complement that project through entailment-canceling operators. Love appears factive because Mo left is inferrable from the standard family of sentences in (10)–(12):
- Jo loves that Mo left.
- Jo doesn’t love that Mo left.
- Does Jo love that Mo left?
But when White and Rawlins (2018) (discussed above) and Degen and Tonhauser (2022) collected projection judgments at scale, they found continuous variation (Xue and Onea 2011; Smith and Hall 2011; Djärv and Bacovcin 2017 also observe similar patterns). Qualitatively, Degen and Tonhauser (2022) argue that there is no clear line separates factive from non-factive predicates. Mean projection ratings vary continuously from pretend (lowest) to be annoyed (highest).
This gradience poses a theoretical challenge (Simons 2007; Simons et al. 2010, 2017; Tonhauser, Beaver, and Degen 2018).
Kane, Gantt, and White (2022) later showed that this gradience is likely due to task effects. They demonstrate that when one applies a clustering model to these data that accounts for noise due to various factors, many of the standard subclasses of factives pop out. Some of these subclasses–e.g. the cognitive factives, which Karttunen (1971) observes to not always give rise factivity–appear to themselves be associated with non-necessary factive inferences.
In this case study, we’ll focus on understanding what gives rise to this gradience. We’ll consider two hypotheses that PDS allows us to state precisely and test against the data collected by Degen and Tonhauser (2021), which uses the same experimental paradigm as Degen and Tonhauser (2022):
The Fundamental Discreteness Hypothesis: Factivity remains discrete; gradience reflects: - Multiple predicate senses (factive and non-factive variants) - Structural ambiguity affecting projection (Varlokosta 1994; Giannakidou 1998, 1999, 2009; Roussou 2010; Farudi 2007; Abrusán 2011; Kastner 2015; Ozyildiz 2017) - Contextual variation in whether complements are at-issue (Simons et al. 2017; Roberts and Simons 2024; Qing, Goodman, and Lassiter 2016)
The Fundamental Gradience Hypothesis: No discrete factivity property exists. Gradient patterns reflect different degrees to which predicates support complement truth inferences (Tonhauser, Beaver, and Degen 2018).
PDS allows us to implement both hypotheses formally and test their predictions against fine-grained response distributions—not just means, but entire judgment patterns including multimodality that might indicate mixture distributions. We’ll show how this approach can be applied to judgment data aimed at capturing factivity using various experimental paradigms (Tonhauser 2016; Djärv and Bacovcin 2017; Djärv, Zehr, and Schwarz 2018; White and Rawlins 2018; White et al. 2018; White 2021; Degen and Tonhauser 2021, 2022; Jeong 2021; Kane, Gantt, and White 2022).
The Need for New Frameworks
These case studies illustrate what we need from a framework connecting formal semantics to experimental data:
Maintain Compositionality: Theories must derive complex meanings compositionally, preserving insights from decades of formal semantic research. We cannot abandon compositionality just because judgments are gradient.
Model Uncertainty Explicitly: The framework must represent both types of uncertainty—resolved ambiguities and unresolved gradience—and show how they interact during interpretation.
Make Linking Hypotheses Precise: We need explicit theories of how semantic representations produce behavioral responses. What cognitive processes intervene between computing a meaning and moving a slider?
Enable Quantitative Evaluation: Theories must make testable predictions about response distributions, not just average ratings. Different theories should be comparable using standard statistical metrics.
As we’ll see in the next section, existing computational approaches like Rational Speech Act (RSA) models attempt to bridge formal semantics with probabilistic reasoning (Frank and Goodman 2012; Goodman and Stuhlmüller 2013). While valuable, these approaches face challenges in maintaining the modularity that makes formal semantic theories powerful. This motivates the development of Probabilistic Dynamic Semantics—a framework that preserves semantic insights while adding the probabilistic tools needed to model gradient behavioral data.
References
Footnotes
We’ll spend a lot of time on Day 4 saying exactly what we mean by discrete here. Karttunen (1971), of course, classically argues that there are predicates that sometimes trigger presuppositions and sometimes don’t. For our purposes, we’ll say that this behavior is discrete in the sense that it’s more like ambiguity than vagueness. That is, we’ll show that uncertainty around factivity displays the hallmarks of resolved uncertainty.↩︎