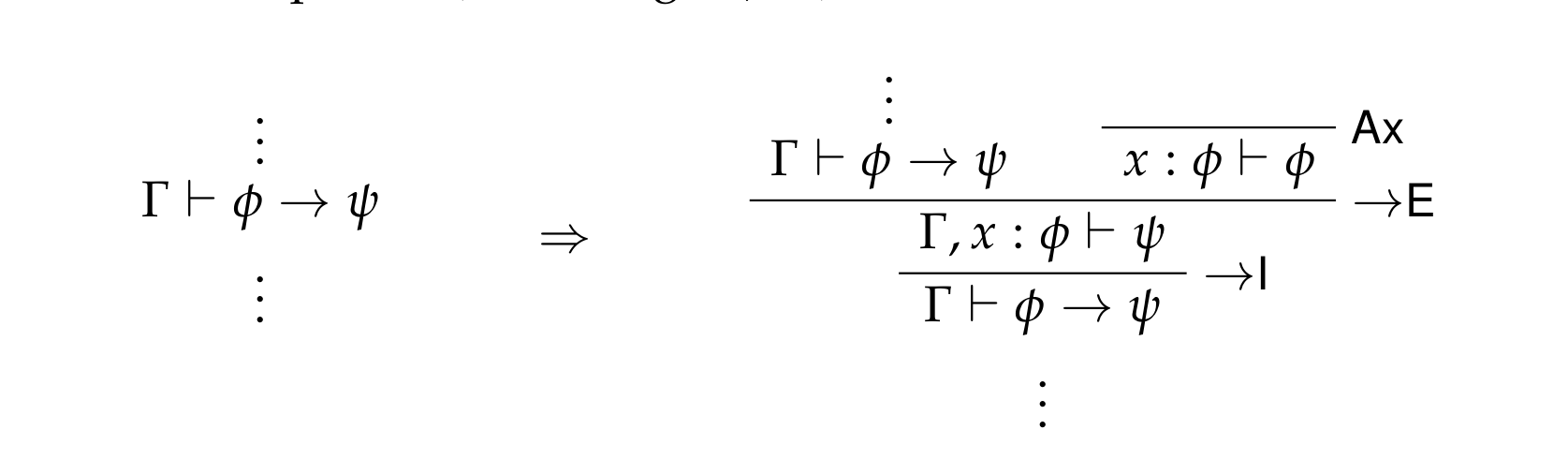Propositional logic: encoding structural rules, and local completeness
Table of Contents
1. Review
Yesterday, we determined a way to encode structural rules (e.g., Weakening, Contraction, Exchange) in our presentation of Intuitionistic Logic in Haskell. We also talked about the notion of local completeness.
1.1. Encoding structural rules
To encode structural rules, we defined a function reorder, which, given some
function that manipulates ways of being in a context (i.e., some f :: forall
φ. In φ γ -> in φ δ), provides a general protocol for reordering the
assumptions in contexts as dictated by f.
reorder :: forall γ δ ψ. (forall φ. In φ γ -> In φ δ) -> Proof γ ψ -> Proof δ ψ reorder f (Ax i) = Ax (f i) reorder f (AndIntro t u) = AndIntro (reorder f t) (reorder f u) reorder f (AndElimL t) = AndElimL (reorder f t) reorder f (AndElimR t) = AndElimR (reorder f t) reorder f (OrIntroL t) = OrIntroL (reorder f t) reorder f (OrIntroR t) = OrIntroR (reorder f t) reorder f (OrElim t u v) = OrElim (reorder f t) (reorder g u) (reorder h v) where g :: (forall χ. In χ (Cons φ1 γ) -> In χ (Cons φ1 δ)) g First = First g (Next i) = Next (f i) h :: (forall χ. In χ (Cons φ2 γ) -> In χ (Cons φ2 δ)) h First = First h (Next i) = Next (f i) reorder f (ArrIntro t) = ArrIntro (reorder g t) where g :: (forall χ. In χ (Cons φ γ) -> In χ (Cons φ δ)) g First = First g (Next i) = Next (f i) reorder f (ArrElim t u) = ArrElim (reorder f t) (reorder f u) reorder f TautIntro = TautIntro reorder f (ContrElim t) = ContrElim (reorder f t)
Note that the following additional language extensions are required for the above to compile:
{-# LANGUAGE RankNTypes #-} {-# LANGUAGE ScopedTypeVariables #-}
For example, we can now define the following functions that encode particular versions of weakening, exchange, and contraction:
weaken1 :: Proof γ ψ -> Proof (Cons φ γ) ψ weaken1 = reorder Next contraction1 :: Proof (Cons φ (Cons φ γ)) ψ -> Proof (Cons φ γ) ψ contraction1 = reorder f where f First = First f (Next First) = First f i = i exchange1 :: Proof (Cons φ (Cons ψ γ)) χ -> Proof (Cons ψ (Cons φ γ)) χ exchange1 = reorder f where f First = Next First f (Next First) = First f i = i
1.2. Local completeness
Each of the connectives with both elimination and introduction rules exhibit the property of local completeness in Intuitionistic Logic. For any given connective, what this property essentially says is that its elimination rules are strong enough for its introduction rules. That this is true can be shown by introducing proof detours: for any judgment in a proof whose consequent has some particular connective as its main connective, that judgment can be replaced with a sub-proof which uses the elimination rule(s) to take apart the connective and uses the introduction rule(s) to build the original formula back up again. In effect, if you take apart a connective using the elimination rules, you're always left with enough pieces to rebuild the formula.
Local completeness is witnessed by the following schematic proof expansions; i.e., introductions of detours. In each case, the simpler proof is on the left, and the expanded proof with the detour is on the right.
1.2.1. Conjunction rules
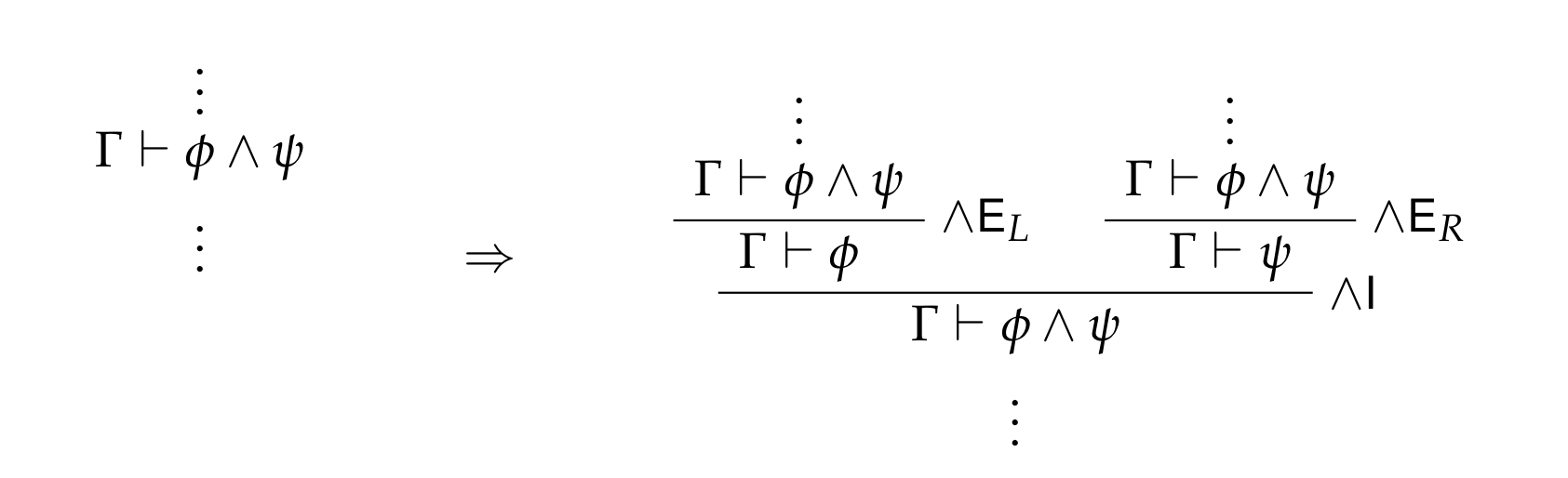
1.2.2. Disjunction rules
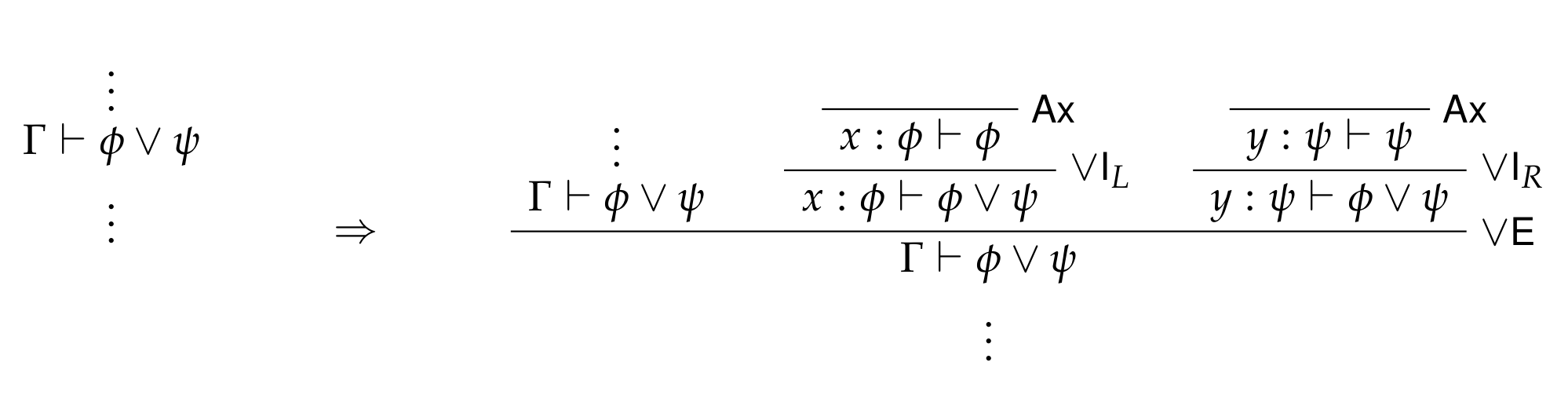
1.2.3. Implication rules